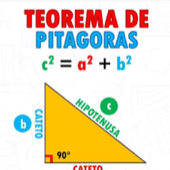
Descubrió que para un triángulo rectángulo (con uno de los ángulos igual a 90°), el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados: a2+b2=c2.
Son aquellos números que además de ser divisibles por ellos mismos y la unidad, también son divisibles por otros números.
“La relación que yo establezco con mi sombra es la misma que la pirámide establece con la suya”.
Propuso las reglas para conocer la divisibilidad de cualquier número.
Introdujo un simbolismo algebraico muy elemental al designar la incógnita con un signo que es la primera sílaba de la palabra griega arithmos, que significa número.
Se puede utilizar para hallar longitudes en donde intervienen triángulos rectángulos.
Construida a partir de axiomas, cuya validez se obtiene por procedimientos lógicos.
Propuso la definición de función numérica como una correspondencia cualquiera entre dos conjuntos de números, que asocia a cada número en el primer conjunto un único número del segundo.
Demostró que el conjunto es infinito. Es decir, no existe un número primo más grande que todos los demás, siempre que halles uno podrás encontrar otro mayor.
Demostró una propiedad de triángulos planos y la correspondiente propiedad de triángulo esférico conocida como el regula sex quantitatum.