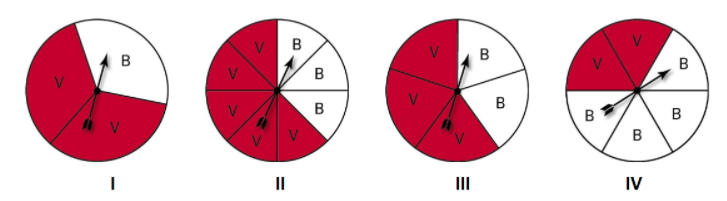
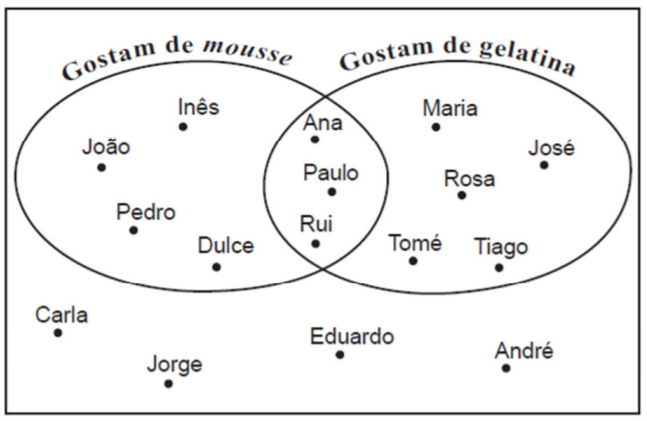
9.
Cinco amigos, a Ana, o Bruno, a Carla, o David e a Elsa, foram à praia. A certa altura, decidiram jogar voleibol de praia. Como as equipas são de pares, vão sortear, ao acaso, um dos cinco amigos para ser o árbitro. Qual é a probabilidade de a Ana ser selecionada? Apresenta o valor pedido na forma de percentagem.